Predicción de resultados de fútbol | Parte 1
Es 06 de Noviembre del 2018 y estoy regresando a casa después de haber participado en el DevFest CR 2018 organizado por la comunidad GDG Pura Vida en este evento estuve participando en nombre de la comunidad GDG Managua con una charla + taller sobre inteligencia artificial, en la cual expliqué un poco en qué consiste, agregando a algunos ejemplos.
Intro
En el año 2017 se cumplió el vigésimo aniversario de la publicación de uno de los modelos de predicción de resultados de fútbol más famosos: el Dixon & Coles, basado en la distribución de Poisson y publicado en 1997.
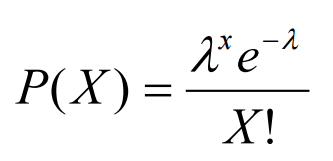
En el artículo original de Dixon & Coles se realizaron algunos ajustes extras para refinar los resultados cuando sus marcadores son bajos, así como que los parámetros de los equipos fueran dinámicos.
La distribución de Poisson es una distribución discreta (enteros) que nos dice la probabilidad de que se produzcan un número determinado de sucesos en un período de tiempo. En nuestro caso, la duración de un partido de fútbol (90 min). El número de sucesos que queremos calcular es “número de goles marcados por el equipo X”. Para ello, debemos alimentar el modelo con el número medio de sucesos, es decir, la cantidad de goles que el equipo debería marcar según sus partidos anteriores.
Procedimiento
Es un modelo muy sencillo de aplicar. Se apoya en el cálculo de medias de goles para cada equipo. Para dotar de mayor realismo al modelo se calculan medias separadas para el rendimiento de los equipos jugando como local y cómo visitante. Por tanto, necesitamos:
- Media de goles marcados por el equipo local, actuando como local ( Hf ).
- Media de goles recibidos por el equipo visitante, actuando como visitante ( Ac ).
- Media de goles a favor de los equipos locales de la liga ( THf ). Esto es equivalente a la media de goles en contra de los equipos visitantes de la liga ( TAc ).
- Media de goles a favor de los equipos visitantes de la liga (TAf). Esto es equivalente a la media de goles en contra de los equipos locales de la liga ( THc ).
- Media de goles marcados por el equipo visitante, actuando como visitante ( Af ).
- Media de goles recibidos por el equipo local, actuando como local ( Hc ).
Puesta en marcha
Para este ejemplo usaremos los datos de la temporada 2017-2018 de la liga española. Tomemos como referencia el partido Celta – Real Madrid de la jornada 18:
El Celta (Local)
- Media de goles marcados por el Celta como local durante esta temporada ( Hf ): 1.38
- Media de goles marcados por el Celta ( Hf ) respecto a la media de goles marcados por los equipos de la liga como locales ( THf ), lo cual nos da una medida de su fuerza atacante relativa ( Hf/THf ): 1.38 / 1.49 = 0.92 ( Hf_r )
- Equipo que rinde un 8% peor que la media de la liga.
Nota: Tenemos que hacer este procedimiento para todos los equipos.
El Madrid (Visitante)
- Media de goles recibidos por el Real Madrid como visitante ( Ac ): 0.71
- Media de goles en contra del Real Madrid ( Ac ) respecto a la media de goles recibidos por los equipos de la liga como visitantes ( TAc, por construcción es igual a THf ), lo cual nos da una medida de la fuerza defensiva del Real Madrid como visitante ( Ac/TAc ): 0.71 / 1.49 = 0.48 (Ac_r )
- Este equipo recibe solo el 48% de los goles que suelen encajar los equipos visitantes.
Nota: Tenemos que hacer este procedimiento para todos los equipos.
Ahora necesitamos calcular los goles esperados del equipo local (Celta). Multiplicamos el ataque del equipo local ( Hf_r ) por la fuerza defensiva del equipo visitante ( Ac_r ) y por la media total de la liga de goles locales ( THf ): 0.92 * 0.48 * 1.49 = 0.66 goles. Esto es la media de goles que esperamos que marque el Celta al Real Madrid.
Nota: Tenemos que repetir este procedimiento pero para el Real Madrid.
Generando Marcadores
Una vez que se tiene el número de goles esperados (0.66 Celta vs. 1.719 Real Madrid) hay que obtener las probabilidades de que se produzca cada marcador, para ello utilizamos la distribución de Poisson.
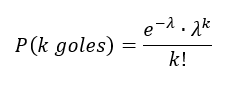
Aplicándolo al Celta:
- P(k goles): probabilidad de que el Celta marque k goles.
- e: número de Euler (2.71…).
- λ: media de goles del Celta (0.66).
Sustituyendo obtenemos estos valores:
- k=0 –> P=51.6%.
- k=1 –> P=34.1%.
- k=2 –> P=11.2%.
Nota: Tenemos que repetir este procedimiento pero para el Real Madrid.
Finalmente, se multiplican ambos sucesos independientes: la probabilidad de que ambos equipos marquen 0 goles (0 – 0) es: 0.516 * 0.179 = 0.092 (9.2%). Y asi podemos ir calculando la probabilidad de diferentes marcadores. En el siguiente post, veremos como simplificar este proceso.
Gracias por leer esta entrada, y si fue de tu agrado, no olvides compartir. Puedes leer la siguiente parte aqui.